Vorhilfe - Kostenlose Kommunikationsplattform für gegenseitige Hilfestellungen
URL: http://www.englischraum.de/vorkurszettel?id=127
| Lineare Algebra I/II, Vorkurs, | www.matheraum.de Lineare Algebra Aufgabenblatt 5 Abgabe: So 18.03.2012 19:00 | 11.03.2012 |
| Die Übungsaufgaben beziehen sich auf das Buch "Lineare Algebra" von Gerd Fischer bzw. auf das Inhaltsverzeichnis, das in der Kursbeschreibung zu finden ist. Die Übungsaufgaben (i.d.R. zu immer einem neuen Kapitel im Buch) können bequem in einer Woche gelöst werden. | ||
| Aufgabe 1 | ||
| V-1: Sei V ein K-VR und (i) B ist eine Basis von V. (ii) B ist maximal linear unabhängig. (iii) B ist ein minimales Erzeugendensystem. (iv) Jeder Vektor v aus V gestattet eine eindeutige Darstellung durch Vektoren aus B. | ||
| Aufgabe 2 | ||
V-2: Bestimmen Sie die Menge T aller t aus 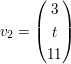 und und 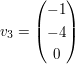 ein Erzeugendensystem von ein Erzeugendensystem von | ||
| Aufgabe 3 | ||
| V-3: a) Zeigen Sie: Aus jedem endlichen Erzeugendensystem eines VR V kann man eine Basis auswählen!
b) Zeigen Sie: Alle Basen eines VR V haben die gleiche Dimension. c) Bildet V = 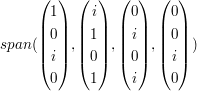 einen VR über einen VR über | ||
| Aufgabe 4 | ||
| V-4: a) Zeigen Sie: Ist W ein Untervektorraum eines endlich erzeugten Vektorraums V, so ist auch W endlich erzeugt und es gilt dim W b) Beweisen Sie den Basisergänzungssatz: Zu einem System linear unabhängiger Vektoren | ||
© Copyright 2003-25 www.englischraum.de
Der Inhalt dieser Seite kann -- sofern nicht anders lautend gekennzeichnet -- durch jedermann gemäß den Bestimmungen der Lizenz für Freie Inhalte genutzt werden.
Der Inhalt dieser Seite kann -- sofern nicht anders lautend gekennzeichnet -- durch jedermann gemäß den Bestimmungen der Lizenz für Freie Inhalte genutzt werden.